How was this made? See Numerical Algorithms, An efficient algorithm for accelerating the convergence of oscillatory series, useful for computing the polylogarithm and Hurwitz zeta functions, Volume 47, Number 3 / March, 2008 pp 211-252.
Click here to view on it's on page (MP4, 25 MBytes) or view it on YouTube!

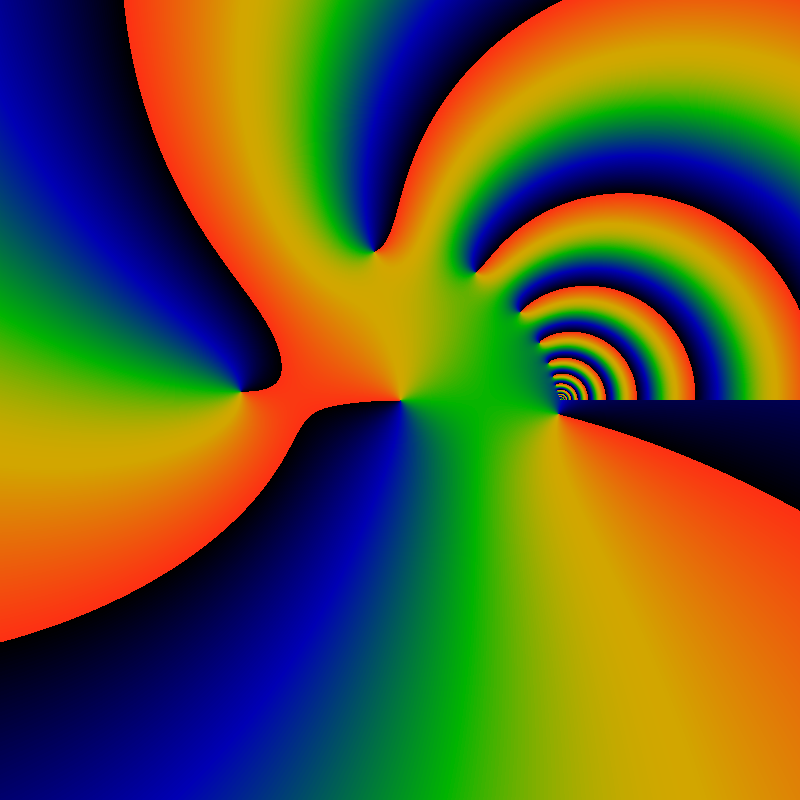
The above shows the polylog on the complex z-plane, for fixed s=0.5+i14, which is not far from the first non-trivial Riemann zeta zero at s=0.5+i14.13. The image is centered on z=0, and ranges over the interval [-2.5,+2.5] in the real and imaginary z-axes (the movie uses [-3.5,+3.5]). Colors indicate the phase: black indicates a phase of -pi, green a phase of zero, and red a phase of +pi. A sharp red-black transition is just the phase jumping from +pi to -pi. The phase wraps by a full two pi around the zeros of the polylogarithm. The zero Lis(0)=0 is clearly visible in the center of the image. Many additional zeros are arranged on an approximate circle near |z|=1. These accumulate at the branch point at z=1 on the right hand side. The discontinuity from z=1 extending to the right is the branch cut. Just underneath the branch cut a lone zero is visible: this is a Riemann-zero-to-be. As s is slowly changed from s=0.5+i14 to s=0.5+i14.134725, this zero will slide upwards, and hit the branch point precisely. This movement is clearly seen in the animation.
Writing s=0.5+it, these zeros circle the origin as t changes. Whenever t is a Riemann hypothesis zero, these zeros pass through the branch point at z=1 on the complex plane. This can be seen clearly in the movie: observe what happens as the frame counter passes each RH zero. The first few are at 14.134725, 21.022040, 25.010858, 30.424876, 32.935062, 37.586178, 40.918719, and so on.
The Riemann hypothesis states that every (non-trivial) zero will hit the branch point at z=1 as it loops along the polylog complex plane. Each zero you see here, on the polylog complex plane, is a future Riemann zeta zero, in the making. It has to loop around the origin first, as seen in this movie, and then hit the branch point at z=1. Every zero you see here is a Riemann zero; the RH would be false if any of them failed to hit z=1.
Riemann zeros also pass through the point z=-1, but so do the zeros of the Dirichlet eta: solutions to 0=2s-1; see, for instance, frame number 2 pi/ln(2)= 9.0647.
The horizontal discontinuity in the middle, extending to the right, is a branch cut, extending from the branch point (essential singularity) at z=+1. One may perform an analytic continuation through it, to reach other sheets. A precise form of the continuation, and its monodromy, is given in the Polylog and Hurwitz zeta algorithms paper. A more detailed and precise discussion of the movies shown on this page is given in the Polylog and Riemann Hypothesis paper. This paper provides details for the relationship to the RH. This includes refining the RH into a strong and weak form. This opens up a new route to proving RH: one would need to show that certain polylog "varieties" are "entire" in a certain sense. Each "variety" is given by the solutions of Lis(z)=0/ These give functions z(s), one for each polylog zero. If there is a one-to-one correspondence between Riemann zeros and these varieties, then each variety is "entire" in a certain sense. If RH fails to hold, then there cannot be a one-to-one correspondence. Of course, I don't know how to prove such a thing. If I did, I'd be busy scribbling down details and claiming prizes and fame.
The left image shows the sheet that results from winding around z=1 in a right-handed manner. There are two branch cuts here, one extending from z=0 and another from z=1 and both have been arranged to extend to the right. Thus they overlap; this should not cause confusion, as there is not much going on in this animation. Notice how the first zero crosses into this sheet, as s moves from s=0.5+i14 to s=0.5+i15. This first zero continues to rotate counterclockwise on this sheet, and is joined by additional zeros at s=0.5+i21, s=0.5+i25, etc. As these rotate, they move onto the next sheet and the next, disappearing into the branch cut.
The right image shows the sheet that results from winding around z=1 in a left-handed manner. Again, there are two branch cuts here, but this time arranged so that the cut from z=+1 extends to the right, while the cut from z=0 extends to the left. The red-black transitions, indicating a phase change from +pi to -pi, seem to spiral in a bit more tightly. Presumably, these spirals get a bit tighter, with each successive sheet, but otherwise wrap around this branch point, unto infinity. Increasing tau is an unwinding.
Each image is centered on z=0, and runs over the interval [-3.5,+3.5] in both the real and imaginary directions. Computation requires from 200 to 400 binary digits of precision, depending on the value of s. This is a lower bound on the precision needed to get nice-looking images; less than this results in severe visual artifacts. Source code can be found on github: The Anant math library for analytical number theory, and Linas' Analytical Combinatorics/Dynamical Systems Diary.
Another curiosity, visible on both the s=0.5+i tau and s=1.1+i tau movies is how a zero leaves behind a shadow, even as it circles onto the next sheet.
Each image is centered on z=0, and runs over the interval [-1.5,+1.5] in both the real and imaginary directions.
This allows one to conclude that the zeros of the polylog form a two-dimensional variety. Labeling each zero with an integer m, there is a function zm(s) such that Lis(zm(s))=0 for all s in the complex plane (barring the branch points, of course).
The bottom half-planes on all three animations differ, although, due to "optical" illusions (exponentially small differences), the left and middle bottom halves eventually look the same. The differences can be clearly seen when 0 < tau < 2; after that, the left-bottom and middle-bottom start to look exactly the same (up to exponentially small differences, not visible with naive pixel color-coding.)
The left-most panel plays another trick on the eyes: the cut from z=1 "disappears" visually after about tau=2. It is still there, but the delta across the cut is exponentially small: the delta goes as exp(-tau) and becomes invisible.
Adding to the confusion is the structure of the polylog monodromy: things on different sheets look quite similar to one another. The left-most animation shows this particularly strongly. For example, at 9 < tau < 12, the left-most animation shows a zero emerging from the cut. That zero looks almost identical to what is on the principal sheet. Yet it is not! Where did it come from? Well, from another sheet (glued along the left-hand cut) that is also spewing zeros. If we were to analytically-continue to that sheet, it would look a lot like the principal sheet. But different, as it would have two cuts, not one. The monodromy is quite the mess. There's a lot of duplicitous behavior, here. Caveat Emptor.
Staring at the left-most panel during the begining of the movie (up to about tau=25 or so), it is clear that there is a cut, starting at z=0 and extending to the left. For frames with tau greater than about 30, the portion of the cut between z=0 and z=-1 "fades away", with no visual distinction across sheets. The cut from z=-1, travelling leftwards, remains prominent. This is another optical illusion.
There's also some interesting funny-business going on in the range of tau=0 to 3, where zeros dance around in an unexpected way, before they settle down to their conventional spiralling pattern.
In short, this animation rewards repeated viewing.

Polylogarithm - The Movie!!!
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.