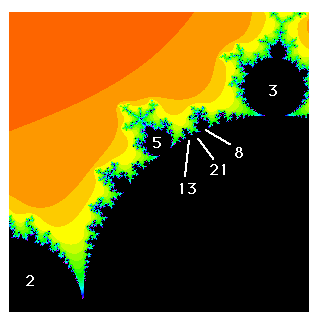
Figure 11. The Fibonacci sequence: 1, 2, 3, 5, 8, 13, ...
The ideas in the previous section allow us to show the presence of the Fibonacci sequence in the Mandelbrot set. Forget for the moment about the rotation numbers and concentrate only on the periods of the bulbs (the denominators). Call the cusp of the main cardioid the ``period 1 bulb.'' Now the largest bulb between the period 1 and period 2 bulb is the period 3 bulb, either at the top or the bottom of the Mandelbrot set. The largest bulb between period 2 and 3 is period 5. And the largest bulb between 5 and 3 is 8, and so forth. The sequence generated (1, 2, 3, 5, 8, 13,...) is, of course, essentially the Fibonacci sequence. See Figure 11.

Figure 11. The Fibonacci sequence: 1, 2, 3, 5, 8, 13, ...
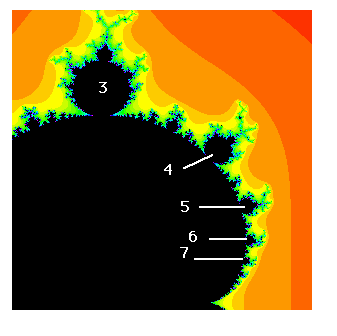
Figure 12. The Devaney Sequence: 1, 2, 3, 4, 5, 6,...
 8 Summary (Next Section)
8 Summary (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 6 How to Add (Previous Section)
6 How to Add (Previous Section)