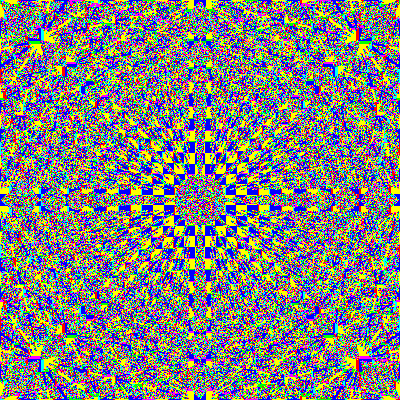Sinai's Billiards
Sinai's Billiards (Lorentz Gas) is a term referring to the study
of the chaotic
dynamical properties of hard elastic balls (read on for a less
technical translation). One of the early and
astounding results of this study is that a gas of two hard balls
is strongly ergodic (i.e. the gas obeys the Boltzmann hypothesis
and becomes stochastic, allowing the basic laws of thermodynamics
to hold true and be applicable). This is a truly amazing result:
you don't need millions of atoms to have a system that behaves
stochastically: two atoms are enough.
What's a 'hard elastic ball', I hear you saying, and why is this
interesting? A 'hard elastic ball' is just what it sounds like:
think of steel ball bearings or BB's, something that bounces very
well and is very hard. The study of how they bounce is interesting
at several levels. At a very basic level, this should remind you
of the 'ideal gas' as studied in high-school physics class: you
are taught to envision a bunch of round, bouncy atoms all bouncing
around (randomly) in a box. So its kinda interesting to ask how
things bounce around. But what really makes this an interesting
problem is that its a doorway to much much deeper mysteries
about the universe, as explained in the 'digression' below.
Below, we present a series of pictures that visually show this
result, by ray-tracing a simple cubic crystalline lattice. We
put 'atoms' or mirrored balls in the lattice, and then trace
a ray of light through the lattice. We then look at lattices of
different sizes: only a few atoms, or hundreds, or zillions.
Because of the periodic boundary conditions, this problem is
identical to one where we put a reflective ball in the center
of a mirrored six-sided cube. We stop ray tracing when the ray
has bounced some number of times off the walls.
(That reflective vs. toroidal boundary conditions make no
qualitative difference is illustrated at the bottom of this
page).
 To better illustrate where the rays are going, the balls are not
perfectly shiny, they absorb some of the light with each reflection.
In addition, to get a sense of direction, we've set it up so that
whenever the ray exists through the left or right side of the
cell, it looses some redness. Think of the sphere as having
some red light filters on either side of it. Above and below are
green filters, and in front and behind are blue filters.
So based on the color of the light, we can tell where it came
from.
To better illustrate where the rays are going, the balls are not
perfectly shiny, they absorb some of the light with each reflection.
In addition, to get a sense of direction, we've set it up so that
whenever the ray exists through the left or right side of the
cell, it looses some redness. Think of the sphere as having
some red light filters on either side of it. Above and below are
green filters, and in front and behind are blue filters.
So based on the color of the light, we can tell where it came
from.
 Notice that the bigger the lattice, the more the light tends
towards grey. The more times a light ray bounces off a sphere,
the more randomized its direction becomes. The more random, the
grayer the image. This visualizes the transition to ergodic
behavior: with each bounce, things get more mixed up, until
finally there is nothing but a fog.
Notice that the bigger the lattice, the more the light tends
towards grey. The more times a light ray bounces off a sphere,
the more randomized its direction becomes. The more random, the
grayer the image. This visualizes the transition to ergodic
behavior: with each bounce, things get more mixed up, until
finally there is nothing but a fog.

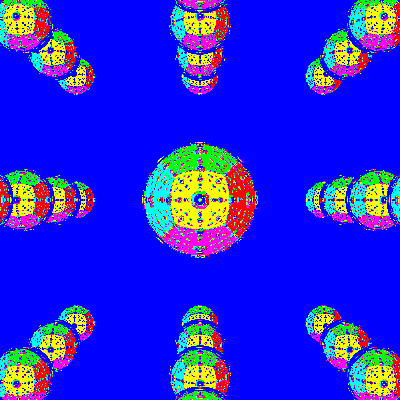
The chaotic nature of the billiards is even more strikingly
apparent if we look at where a ray came from. In the picture
below, we've colored the walls of the cube different colors.
We can see these walls reflected in the sphere in the center.
You can clearly see the perspective fore-shortening of the
walls of the cube, and you can see clearly how the sphere
is reflecting the walls.
 The next picture shows two bounces. First, we notice that the
sphere reflects images of its neighboring spheres. We see
also that the inside of the cube seems to be more complicated.
The walls of the cube are reflecting each other: the walls
are showing a reflection of the walls.
The next picture shows two bounces. First, we notice that the
sphere reflects images of its neighboring spheres. We see
also that the inside of the cube seems to be more complicated.
The walls of the cube are reflecting each other: the walls
are showing a reflection of the walls.
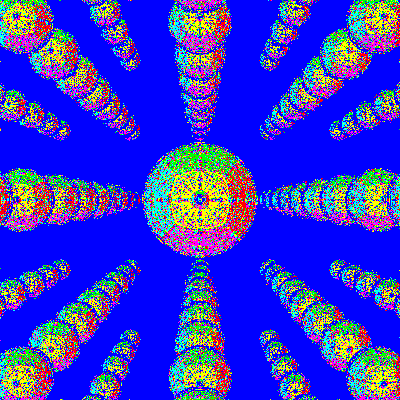
 The next image extends the process to four bounces. We can
see that the reflections of the reflections are starting to
get pretty complex.
The next image extends the process to four bounces. We can
see that the reflections of the reflections are starting to
get pretty complex.

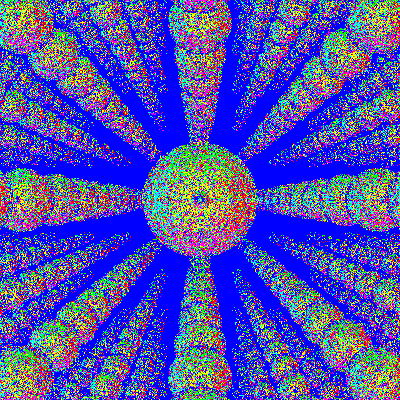
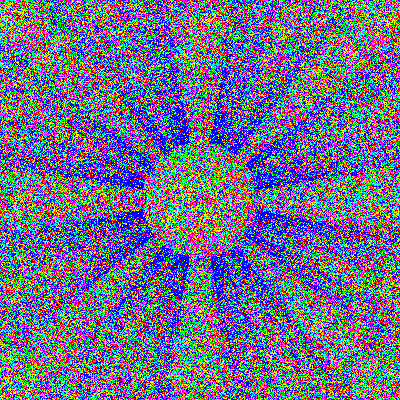
 The last two images show 10 and 80 bounces.
Uh-oh. In the 10-bounce image, we can still see spheres.
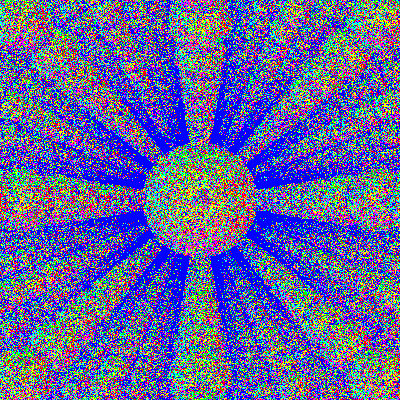
In the 80-bounce image, all traces of the spheres have been
erased. Looks like random noise to me; its all mixed up.
If you created a super-high resolution image of eighty bounces,
and used a magnifying glass to examine it, you *might*
be able to pick out the fact that there are still spheres
in there. But that is missing the point: another bounce or
two, and even that image would be hopelessly stirred up.
The transition to chaos is exponential: in a short amount of
steps, in a finite time, you reach a practical limit that
cannot be overcome. The operative phrase here is "finite time'.
The last two images show 10 and 80 bounces.
Uh-oh. In the 10-bounce image, we can still see spheres.
In the 80-bounce image, all traces of the spheres have been
erased. Looks like random noise to me; its all mixed up.
If you created a super-high resolution image of eighty bounces,
and used a magnifying glass to examine it, you *might*
be able to pick out the fact that there are still spheres
in there. But that is missing the point: another bounce or
two, and even that image would be hopelessly stirred up.
The transition to chaos is exponential: in a short amount of
steps, in a finite time, you reach a practical limit that
cannot be overcome. The operative phrase here is "finite time'.

Digression
At this point in time, physicists are engaged in a fundamental
debate pitting the philosophical ideas of 'emergent behavior'
and 'reductionism' against each other.
On the one hand, (according to the dogma of reductionism), air
is made out of atoms (quantum mechanical ones at that), which
are made out of smaller pieces, and so on. On the other hand
(according to the dogma of emergent behavior), out of this
gas of atoms appear the laws of statistical mechanics; and the
laws of statistical mechanics don't seem to care at all that
the atoms were quantum mechanical. Neither dogma explains very
well (ok, doesn't really explain at all) how we got from here
to there. The problem is that we don't really understand how
to get from deterministic, time-reversible equations of motion
for point particles to the smooth, density-based, time-irreversible
equations of statistical mechanics. Where did the time
symmetry go? How did point particles become a smooth continuum?
Most textbooks give a hand-waving explanation about how
Avogadro's number is so big, and maybe a derivation of the
Gaussian distribution as the large-number limit of the
Poisson distribution. Tastes great, less filling.
The surprise of Sinai's billiards (as so amply illustrated
in these pages) is that you don't need a million atoms to
get stochastic behavior, you only need two. Furthermore,
the loss of determinism is not due to some 'random averaging',
but is a fully deterministic, chaotic process: it looks like
chaos one sees in fractals.
Several mysteries remain. First, what happens when we replace
the hard elastic balls with quantum-mechanical dispersive waves?
After all, we do believe that atoms are quantum mechanical, and
we do know that if we put a single atom in a box, localize it
to one spot, close the box and wait, then its wave function will
slowly expand to fill the box. If we put two in, well, the same.
Is this problem completely unrelated to Sinai's billiards? It
seems to be, but is there something more subtle going on?
A related mystery is brought up by Dean Driebe's derivation of time
asymmetry from the Bernoulli map. The derivation is important,
but the explanation seems shallow: one picks one representation
(in the sense of 'representation of a group') and gets reversible
particle/point dynamics, and one picks a different representation,
and gets time-asymmetric chaotic evolution. This works great in
the pure, mathematically abstract realm of the Bernoulli transform
and Baker's map. But when applied to the physics of a hard gas,
its disconcerting: the physics depends on the representation.
This disconcerting feeling is not new: quantum mechanics is
rife with it: the time evolution of a quantum state depends on
how it was prepared, which is a way of saying that it depends on
the representation. (e.g. 'singlet', 'triplet' are different
representations of the rotation group). We got used to this
notion in quantum mechanics, but its once again disturbing to
bump into this again when dealing with chaotic systems.
Its kind of like state reduction in quantum measurement:
one can talk about the chaotic evolution of the billiards
system, but when one asks 'where's the billiard ball right
now?' one must leave the time-asymmetric representation behind,
and hop back to the time-symmetric, deterministic point-particle
representation. Very discontinuous. Makes you wonder what
reality really is. How can reality just change like that,
on a whim, as it were?
The fourth mystery invokes the words 'quantum mechanics' again,
but in a different way than above. The 'quantum measurement problem'
to this day remains a 'problem', or is at least opaque. Measurements
seem to happen when a quantum particle interacts with a many-body
system, whether (for example) silver on a film plate, or condensation
in a cloud chamber. Well, Sinai's billiards are a sort-of realistic
model for crystals and gases; is there perchance any connection at
all between quantum measurement, and the goings-on with billiards?
Maybe there is none at all, but where else can we start looking
for a suitable foundation for the many-body nature of wave-function
collapse?
Miscellaneous Technical Results
The mean free path of a ray in this lattice is presented
here.
Atlas
Below follows the entire atlas of images, for a variety of
ball sizes and lattice sizes. We provide this atlas for all
of the usual reasons: you, the reader, no doubt is curious as
to what might happen if a parameter or two was varied. The
atlas provides a simple visual guide to these variations.
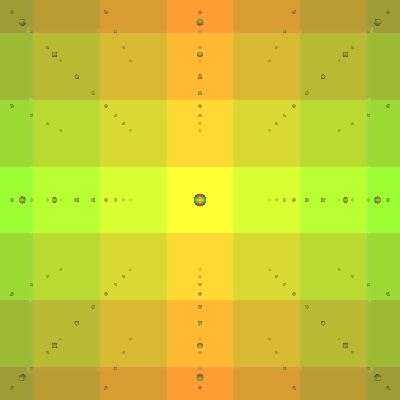
In the first round of images,
the ball radius is equal to 0.3 of the size of the fundamental
basic cubic cell. First, we start with the image of one ball:

Then a two-deep lattice:

Then a three-deep lattice:

Then a four-deep lattice:
Notice the reflections of the other balls are showing in
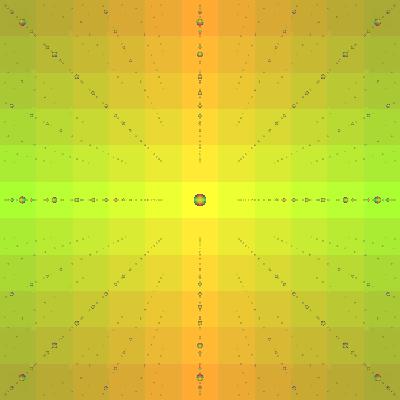
each of the balls.

And so on. Note how the reflected image in the sphere
keeps getting more and more complicated. That is the other
way to envision the transition to chaos: two rays of light,
initially very close to each other, hit the sphere, and bounce
off in slightly different directions. But as we can see, the
reflection of a reflections of a reflection gets more and more
complicated and filigreed: even close-by rays will hit on
different reflections. Eventually, the pattern becomes so
complicated, it just turns to mud.














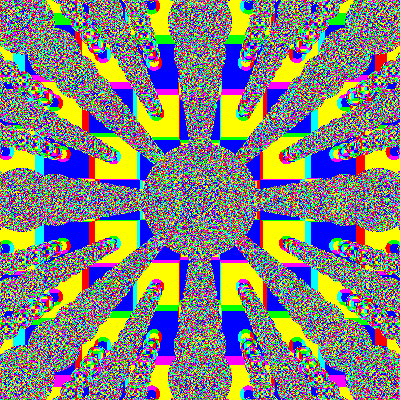

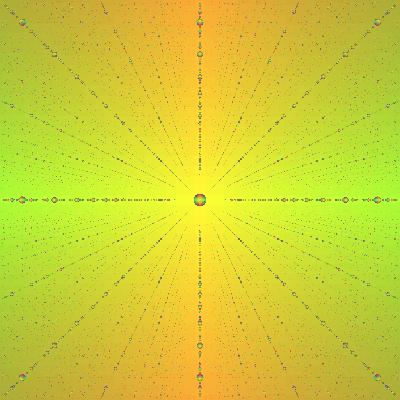
Radius 0.4
We can see that larger sphere's just mix things up a whole lot
quicker. The images below get muddy, quickly.







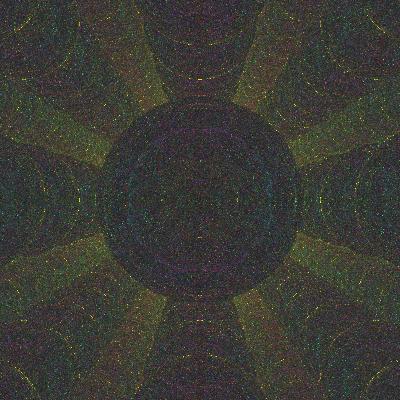








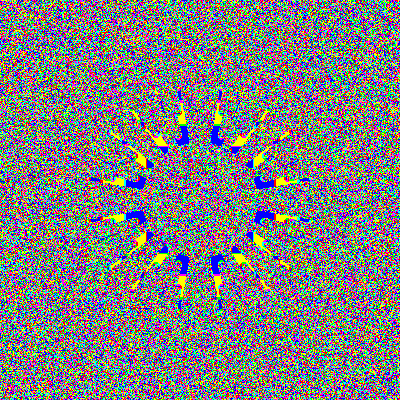
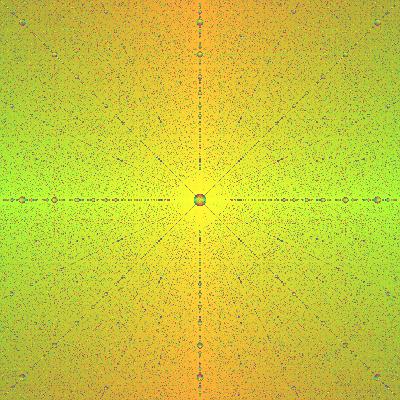
Radius 0.2
Smaller sphere's aren't as quickly mixing as the big ones.
But with a big enough lattice, they get there eventually.
Notice the diagonal lines appearing in the image. These lines
correspond to the iterated Bernoulli map.





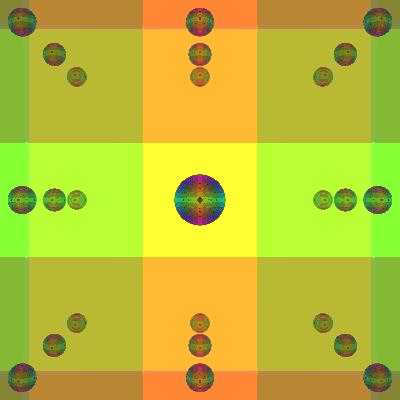
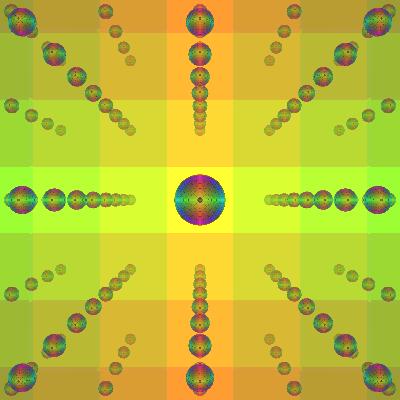











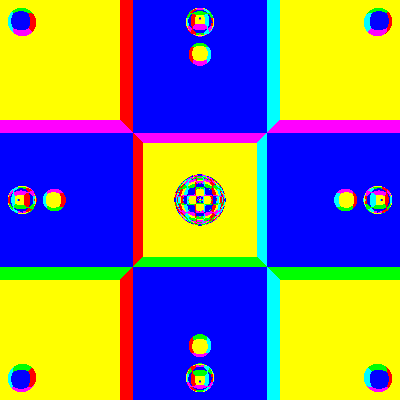
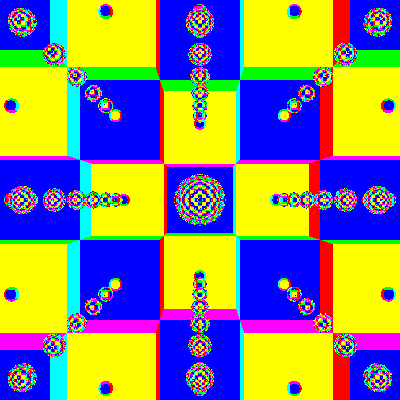


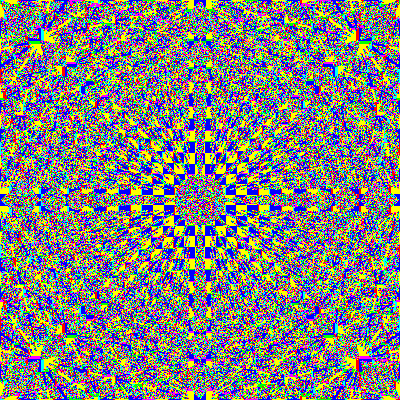
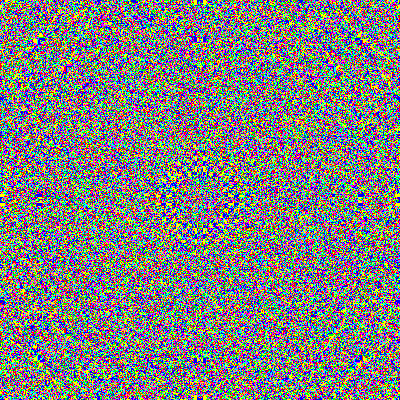
Radius 0.1
Some really small spheres. Just like above, the key word is
'eventually'. With small spheres, the mean free path can be
very very long. But the spheres, no matter how small, still
introduce hyperbolic trajectories, and as we know, anything
hyperbolic is chaotic.





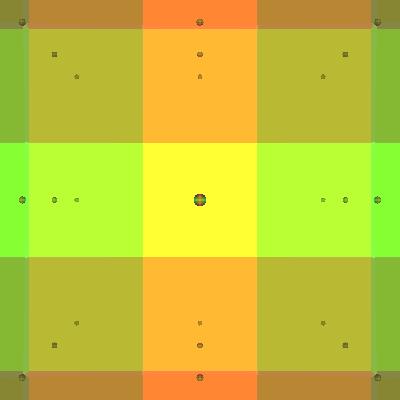


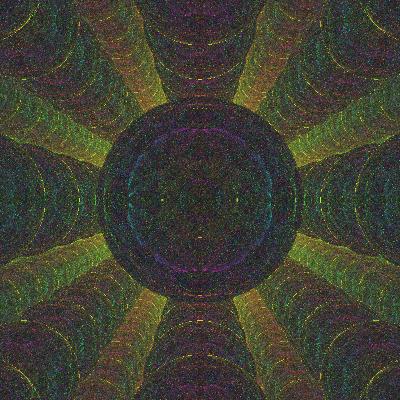
Toroidal Boundary Conditions
All of the above images were computed using reflective boundary
conditions. What if we had used toroidal boundary conditions
instead? That is, what if we ray-traced a lattice of 'real' spheres
laid out on a 'real' lattice, instead of a mirror-land of
reflections? The pictures below show the progress of rays in
a true, non-mirrored lattice. As you can see, it makes no
qualitative difference.
Note how the background is a uniform color,
not a checkerboard. The background still looks tiled, and it
may be worth understanding why. When I carve out a finite sized
lattice, what I carve out is roughly spherical. Think of
a sphere assembled from toy Lego blocks. What looks like
'tiles' are in fact just the side-walls of the more distant
cells.







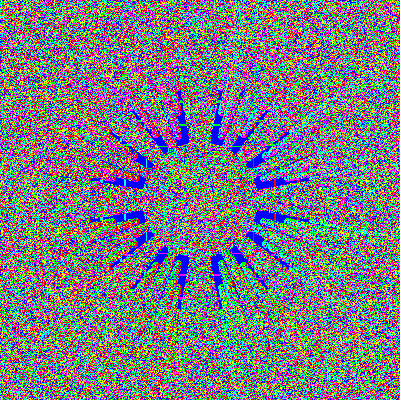

'Ahah', you might think, 'but what if we worked with a true cube?'
That should make the tiling effect go away. And as the pictures
below show, this does indeed seem to simplify things, at least
as first. We can see that much of the apparent complexity of Sinai's
billiards does indeed seem to be due to the boundary conditions.
But in the end, its not the boundary conditions that matter. It
really is the hyperbolic effect of rays bouncing off spheres that
makes classical trajectories through a lattice of atoms chaotic.

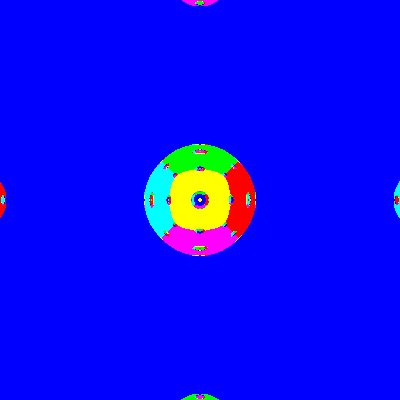
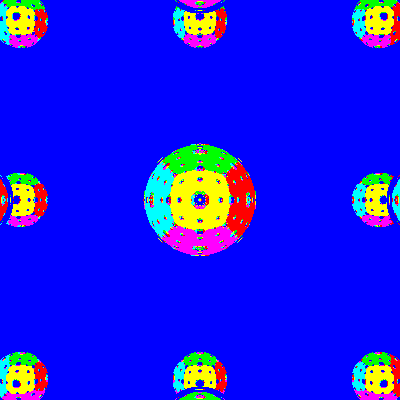
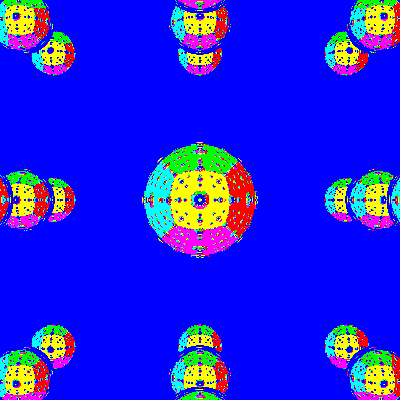
Closing Thoughts
Is it really remarkable that a ray bouncing through a lattice
of balls has a chaotic trajectory? Well, maybe not, for if one
thinks about it, how could it be otherwise? In that case,
the surprise should come when one thinks about passing a wave,
rather than a point particle, through the lattice. As any
high-school student (that didn't sleep through physics class)
knows, waves traveling in a lattice are not chaotic,
but instead exhibit diffraction. You don't need x-rays shining
on a crystal to get diffraction: simple water-wave tanks will
show water waves diffracting off of pilings.
That, in a nutshell, summarizes what happens when one looks
for chaos in the quantum world: one usually finds that the
quantum analog is plain, simple and ordered, and not chaotic.
But this conclusion is misleading.
The quantum version of Sinai's billiards is not textbook diffraction
from a crystalline lattice. The traditional diffraction
calculations make a simplifying assumption: there is only one
interaction, only one bounce, between the incoming and outgoing
rays. This one bounce is what allows the waves to coherently
superimpose. If one allows for multiple bounces, there is a powerful
mixing or decoherence that completely damps the wave.
Indeed, looking at a wave tank, we can see that diffraction is a
'surface' effect. The waves penetrate some depth into the
regular lattice, but they do not penetrate arbitrarily deep.
Diffraction is happening near the surface, where the waves
can penetrate, bounce, and get back out relatively unscathed.
The way to see this by means of a ray-tracing numeric simulation
is to use a Feynmann Path Integral. As a ray bounces through the
lattice, the distance that it travels is kept track of. This distance
is used to compute the phase of the ray as it emerges from the lattice,
using the traditional exp (ikx). Many (randomly generated)
rays can be passed through the lattice, and their phases are summed
as they emerge. One quickly finds that the phases all cancel out
and everything washes out to zero. The quantum analog of Sinai's
billiards appears to be a kind of anechoic chamber, where all waves
are absorbed without reflection.
Open Research Items
- Determine distribution of free paths
- Compare the above to the mean free path of x-rays in crystals
for real-life systems.
- Find literature that discusses penetration depth of waves
in regular lattices.
- Compute similar results for a two-balls hard gas.
Notes & Bibliography
Assorted notes & bibliography.
-
Introduction (from a physicists/mathematicians viewpoint) to
Sinai's Billiards.
-
Chaos in Semiconductor and Optical Billiards introduces the
quantum equivalent of Sinai's Billiards in a two-dimensional
electron gas in Gallium Arsenide. Very curiously, the
magneto-resistance is a fractal that appears to be exactly
self-similar!!
Copyright (c) 2001, 2002 Linas Vepstas

Sinai's Billiards Visualization
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.
To contact Linas, see his
Home Page.
 To better illustrate where the rays are going, the balls are not
perfectly shiny, they absorb some of the light with each reflection.
In addition, to get a sense of direction, we've set it up so that
whenever the ray exists through the left or right side of the
cell, it looses some redness. Think of the sphere as having
some red light filters on either side of it. Above and below are
green filters, and in front and behind are blue filters.
So based on the color of the light, we can tell where it came
from.
To better illustrate where the rays are going, the balls are not
perfectly shiny, they absorb some of the light with each reflection.
In addition, to get a sense of direction, we've set it up so that
whenever the ray exists through the left or right side of the
cell, it looses some redness. Think of the sphere as having
some red light filters on either side of it. Above and below are
green filters, and in front and behind are blue filters.
So based on the color of the light, we can tell where it came
from.
 Notice that the bigger the lattice, the more the light tends
towards grey. The more times a light ray bounces off a sphere,
the more randomized its direction becomes. The more random, the
grayer the image. This visualizes the transition to ergodic
behavior: with each bounce, things get more mixed up, until
finally there is nothing but a fog.
Notice that the bigger the lattice, the more the light tends
towards grey. The more times a light ray bounces off a sphere,
the more randomized its direction becomes. The more random, the
grayer the image. This visualizes the transition to ergodic
behavior: with each bounce, things get more mixed up, until
finally there is nothing but a fog.

 The next picture shows two bounces. First, we notice that the
sphere reflects images of its neighboring spheres. We see
also that the inside of the cube seems to be more complicated.
The walls of the cube are reflecting each other: the walls
are showing a reflection of the walls.
The next picture shows two bounces. First, we notice that the
sphere reflects images of its neighboring spheres. We see
also that the inside of the cube seems to be more complicated.
The walls of the cube are reflecting each other: the walls
are showing a reflection of the walls.
 The next image extends the process to four bounces. We can
see that the reflections of the reflections are starting to
get pretty complex.
The next image extends the process to four bounces. We can
see that the reflections of the reflections are starting to
get pretty complex.

 The last two images show 10 and 80 bounces.
Uh-oh. In the 10-bounce image, we can still see spheres.
In the 80-bounce image, all traces of the spheres have been
erased. Looks like random noise to me; its all mixed up.
If you created a super-high resolution image of eighty bounces,
and used a magnifying glass to examine it, you *might*
be able to pick out the fact that there are still spheres
in there. But that is missing the point: another bounce or
two, and even that image would be hopelessly stirred up.
The transition to chaos is exponential: in a short amount of
steps, in a finite time, you reach a practical limit that
cannot be overcome. The operative phrase here is "finite time'.
The last two images show 10 and 80 bounces.
Uh-oh. In the 10-bounce image, we can still see spheres.
In the 80-bounce image, all traces of the spheres have been
erased. Looks like random noise to me; its all mixed up.
If you created a super-high resolution image of eighty bounces,
and used a magnifying glass to examine it, you *might*
be able to pick out the fact that there are still spheres
in there. But that is missing the point: another bounce or
two, and even that image would be hopelessly stirred up.
The transition to chaos is exponential: in a short amount of
steps, in a finite time, you reach a practical limit that
cannot be overcome. The operative phrase here is "finite time'.